Revista Educare
UPEL-IPB
Barquisimeto, Edo. Lara - Venezuela

Vol. 24 N° 2
Mayo - Agosto 2020

Applied mathematics in crisis scenarios (Covid-19)

Matemáticas aplicadas en escenarios de crisis (covid-19)

Milagros Del Valle Morales Rangel

Atlantis University - USA

ABSTRACT

Applied mathematics is part of undergraduate and postgraduate university education. From this perspective, this essay aims to study the psychological effects, economic and, educational effects upon the population caused by a crisis scenario as COVID-19. The mathematical theories developed in this essay are Chaos Theory, Markov Chains, and Nash Theory. COVID-19 has spread throughout the world, affecting populations, and countries, without distinction of race, economic, political, or socio-cultural position. The impact that COVID-19 has caused on the world population could be measured, in the medium and long term, through changes in psychological behavior, social, health, economic and educational habits. This impact will leave deep traces and moral dilemmas that will permit prioritize which areas address and the political effort directed to each one.

RESUMEN

Las matemáticas aplicadas forman parte de la formación universitaria en pregrado y posgrado. Desde esta perspectiva este ensayo tiene como objetivo estudiar los efectos psicológicos, económicos y educativos ocasionados sobre la población por un escenario de crisis como el COVID-19. Las teorías matemáticas desarrolladas en este ensayo son: Teoría del Caos, Cadenas de Markov y Teoría de Nash. El COVID-19 se ha extendido a través del mundo, afectando poblaciones y países, sin distinción de raza, posición económica, política o sociocultural. El impacto que el COVID-19 ha causado en la población mundial se podrá medir, a mediano y largo plazo, a través de cambios en el comportamiento psicológico, hábitos sociales, de salud, económicos y educativos. Este impacto dejará profundas huellas y dilemas morales como priorizar qué áreas deben atenderse y cuál será el esfuerzo político dirigido a cada una de ellas.

INTRODUCTION

Mathematics frequently are used to analyze theoretical problems. However, they can be used in daily life to makes it easier, understandable, solve problems, and take assertive decision-making. In crisis scenarios, mathematics has helped humanity project, measure, and track the possible causes and effects that these crises or events have over the population. Mathematics also collaborates with different branches of science to find efficient solutions, mitigate effects, and manage resources appropriately.

The COVID-19 pandemic has affected the lives of people worldwide, affecting jobs, school systems, sports, and recreation. Governments have suffered a drastic reduction in their economies, high volatility in stock markets, and a profound impact on health systems. Rarely is considered in the statistics an essential group of the population such as children; however, a large group of children and younger in school ages will feel the change in their style of life, such as taking the class online, reinforce cleaning habits, and recreation habits.

In this essay, essential and complex mathematical theories, such as the Chaos Theory, the Markov Chains, and the Nash Theory, will be used to explain, understand, and project the most appropriate behavior of the population lead a better chance of overcoming the pandemic.

The use of these mathematics theories helps us to obtain the necessary data upon the epidemics spread, and analyze in a theoretical and practical form the endemic and economical graphic models, to study the psychological, economic, and educational effects provoked on the population. It is essential to show that the selected model, the Markov Chains on discrete processes, presents a significant mathematical complexity. Thus, the analysis will be carried out based on the graphs generated by the discrete matrix.

The effects of COVID-19 will be observed and felt over months and perhaps years. Moral dilemmas will arise, thereby prioritizing which areas should be addressed, such as the population health, the economic health of each country, unemployment statistics, and difficulties in accomplishing the scholar curriculum at the end of the scholar year, affecting the school system. The governments should be political and economic efforts and protect the most susceptible and vulnerable population groups such as the elderly and the economically depressed population.

BACKGROUND

Throughout history, humanity has faced several epidemics, which have had a profound impact, changing societies' behavior from ancient Egypt to the twenty-first century. These epidemics include tuberculosis, smallpox, bubonic plague, influenza, acquired immunodeficiency syndrome (AIDS - 1981), Sars (2002), avian influenza (2005), Mers (2012), Ebola (2014) and Zika (2015), to mention just a few.

The epidemics spread maps show a similar behavior or geographical pattern. However, there is a historical discrepancy between the effects caused by them upon the real economy and stock markets. These epidemics have historically caused a significant imbalance in the real economy where governments, small businesses, schools, churches, art centers, and sports centers usually have absorbed huge losses.

Based on statistics of past pandemics, the Center for Disease Control and Prevention published "Community Mitigation Guidelines to Prevent Pandemic Influenza" (CDC, 2017, p. 1–34). Thereby, it suggest the school closures of childcare facilities, elementary and high schools, and higher education institutions to protect the school community and disrupt the transmission of infections by implementing prevention measures, social distancing, and coordinated closure of schools in the most affected areas.

According to the United States Public Health Service (USPHS), from 1918 to 1957, the data collected during pandemic periods showed that the number of cases of infections among children in school-age increased exponentially, due to the high rate of transmissibility between children in schools and from children to adults of their households. Nevertheless, the effectiveness of school closure and social distancing policies was not proven until new studies showed that early school closure could help disrupt pandemic transmission (Chung, 2009, p. 21-26).

On the other hand, the impact caused by the epidemics over stock markets has been very subtle. However, in some cases, it maintained an upward trend in the months following pandemics' onset.

HYPOTHESIS

1. If Governments and societies concerned take join actions and unite for the common benefit by taking appropriate corrective measures, the society will derive maximum benefit (in this initial approach will be using the Nash Theory).
   
   Then, cases of contagion and death would then occur in a smaller proportion. However, significant economic losses will be observed (in the hypothesis verification will be using the Markov Chains, stochastic processes).
2. If the governments and societies concerned assume selfish behavior, where each person thinks only of his benefit, the result will be the minimum benefit for the entire population (in this initial approach will be using the Nash Theory).
   
   Then, there will be a substantial epidemic spread, more cases of contagion, and deaths. However, a high probability of economic fall is keeping, although attenuated (in the hypothesis verification will be using the Markov Chains, stochastic processes).

COVID-19 and analysis of Chaos Theory

COVID-19 has spread rapidly throughout the world. Initially, it emerged as a small viral infection in Wuhan city; however, it increased exponentially, infecting a large part of the population of that city, causing significant deaths and economic damage. This behavior was repeated in each geographical area where the infection appeared, expanding as concentric waves with a common origin in Wuhan city.

This behavior could be explaining from the Chaos theory perspective and the butterfly effect. According to Edward (1996), "as the butterfly effect: in China a butterfly flaps its wings, leading to unpredictable changes in The U.S. weather a few days later" (p. 636-646).

A common factor allows us to relate the COVID-19 epidemic with the Theory of Chaos and the Butterfly Effect expressed by Edward Lorenz. A small disturbance, as the initial contagion by COVID-19 on one side of the world, expands as waves that cause substantial and harmful effects on the other side of the world.

This effect generates repetitive economic and epidemiological behavior patterns in each geographical region where the COVID-19 pandemic occurs, which could also be explaining through fractal models.

Behavior and psychology of the masses

Mass psychology, especially in stock markets, refers to the emotions people have when investing. These emotions are predictable and very noticeable. They are observed daily in the markets through the variations in prices and the graphs. Emotions are shown as an avalanche, ranging between fears to greed.

The COVID-19 pandemic has caused an impact on human psychology, motivated by changes in habits in daily activities. For example, schools have had to cancel assemblies, events, modify the teaching model. Many parents and children have not been able to adapt to space constraints, economic losses, and health. According to the National School Board Association (2020), it is possible an increase in the numbers of teachers and employee absences due to illness in employees and their family members, Additionally, school absenteeism, parental absenteeism from work, and the occurrence of secondary illness in families. The result will be early school closure due to high levels of absenteeism or illness (p. 1-9).

Forced confinement, purchasing power loss, and pre-existed problems in every society and family have exacerbated a depressive outbreak in children, youth, and adults. These have increased in statistics for domestic violence and suicides. According to the American Psychological Association (2020), family confinement in-home may increase intimate partner violence and child abuse. Additionally, disrupted routines and the potential to be contagious with the life-threatening disease may exacerbate mental illness or substance use problems. Another factor to consider has been increasing gun sales. All of them could be a storm to suicide risk (Clay, 2020, p. 4).

At this point, both Chaos Theory and Nash Theory can make significant contributions, explaining how behavior and masses psychology will become a predominant factor searching for solutions that benefit the majority, or failing that, cause more contagion, suffering, and death.

The Chaos Theory allows extrapolating the human psychological factor under the following, “Under innate creativity, there could be an underlying chaotic process it selectively amplifies small fluctuations and shapes them into mind-states coherent, and macroscopic that are experienced as thoughts” (Crutchfield, Farmer, Packard, Shaw, 1994, p. 30).

It is important to emphasize that the essay shows how the psychological impact of containment and isolation measures can be explaining throughout the prisoner's dilemma in Game Theory and Nash Theory, assuming:

Two conspirators in crime are arrested and offered a deal:

If one confesses and testifies against his accomplice, they will let him go, and throw the weight on the other ten (10) years in prison"... "If both remain silent, prosecutors cannot prove more serious charges, and both would spend only a year behind bars for minor offenses. If they both confess, prosecutors would not need their testimony, and both would receive eight-year prison sentences. (Roth, 2004)

Translating this prisoner’s dilemma of the Nash Theory to the current pandemic situation, we find that the proper management, both in the reduction of contagion and in the economic impact will depend on the behavior that the society decides to take.

How to apply the prisoner’s dilemma of the Nash Theory within this situation? In terms of selfishness or solidarity, observing sanitary norms and social distancing, or simply not complying with any norm.

Prioritizing the option that benefits each individual (selfish), to the detriment option that generates common benefit (solidarity), will imply that the COVID-19 pandemic consequences and effects will remain for a more extended period, where prolonged economic deterioration and loss of life could be observing. However, it could be a mitigating factor to keep under control of the dynamic growth of contagions and bring it to a linear evolution.

Similarly, we will observe how the psychological effects will remain for longer, causing additional unwanted emotional damage, such as depression, severe anxiety, panic attack, and increased suicide statistics.

Mitigate COVID-19 expansion. Solution or dilemma?

Although the Coronavirus acted as a trigger in economic, social, and educational deterioration, statistics indicate that accumulated pre-existing elements, in previous years and months, increased bewilderment and slowed down taking adequate measures.

Thus, we can see these patterns in two main parameters: social-educational and economic-financial.

Social and educational: The United States Census Bureau reported in October 2018, a significant discrepancy in the percentage of students enrolled in the school system, determined by the difference in income, family type, and racial group.

Pre-existing factors such as low family income, lack of family support, parents' educational level, family disintegration, belonging to minority racial groups, have accentuated the school dropout in this COVID-crisis19. Besides, new factors are added, such as loss of classes, deficiencies of the school environment, level of learning, and teachers’ and students' difficulties in implementing methodologies that allow continuing academic programs.

In academic teaching, it is crucial to keep in mind that "looking at educational practice and learning from different philosophical, pedagogical, paradigms, models and educational approaches will provide a better perspective and understanding of how the student learns" (free translation from Olivero, 2019, p. 77-91). This recommendation will help mitigate the deficiencies identified in students due to pandemic and social isolation.

Many organizations suggest specials strategies to Prevent the spread of disease, UNICEF published “Key Messages and Actions for COVID-19 Prevention and Control in Schools” (UNICEF, 2020, p. 1-13). That is a Guide to develop plans, take measures, and mitigate the effects of school closures and social isolation of children. To continue educating children at home during the confinement and closure of schools through online education where possible, helping teachers and parents follow up on reading and educational exercises at home, teach and reinforce cleaning habits.

The main objective is to give teachers tools to promote primary health principles, make school attendance more flexible, encourage staying at home, implement remote monitoring control methodologies, implement psychological support programs, and assist vulnerable children and children with special needs.

Economy and stock markets: Making a stock market, fundamental and technical analysis, we could observe a pre-existing factor, during the last eleven years, where the leading indices maintained an upward trend and tiny downward corrections. Beside and no less important, we found the political-financial factors such as positioning in world markets, a reduction over oil production, disagreements between Russia and Saudi Arabia in the energy sector, currencies, and financial systems weakening.

Whether we add to these factors an unexpected element, such as the spread of COVID-19 and the uncertainty it has caused in all areas and sectors, individually and collectively, not only will the impact on stock market volatility be noticeable, but in the whole economy. This impact will leave deep traces and the governments leading and addressing political efforts directed to support the economy and citizen lives. Families and businesses have made significant readjustments, use emergency management, and implement policies to adapt to new job needs and consumption patterns. All of these can be seen in the graphs below.

Markov's Chains SIR model is often used to study epidemics, and infectious processes in populations, thus model graphs allow will project the behavior of the epidemic and its effect on the economy. In a SIR model, the individuals in a population are representing by three possible states: susceptible population, infected population, or population killed by the disease.

Nevertheless, what is The Markov chains theory in discrete-time?

The Markov Chains in discrete-time occur when the variable studied can only take discrete values, and its observation in time is done in discrete instants of time. The stochastic process is represented by X(1), X (), X(3),…, with X(n) being the value of the variable X at time n, with n=1, 2, 3,... the future state of individuals will depend only on their present state. In this case, the probabilities of transition from one state to another are defined by. (Norris, 1998, p. 256)

Expressed as follows in the equation:

pij (n) = P[X(n+1)=j|X(n) =i] i,j=1, 2,..., m

In this case, the selected model is a discrete Markov Chain, since the governments and entities as the Center for Disease Control and Prevention (CDC) in the U.S. have observed and collected data of the individuals affected during the COVID-19 pandemic daily; that is to say, the periods applied are discrete in time. Moreover, the future state of an individual will depend only on his current state, which will generate a discrete matrix.

How we observe in priors paragraph, this model allows simulating behaviors according to the individuals’ states of infection in a population that will be represented by three possible states: susceptible population by COVID-19, infected by COVID-19 population, or population killed by the disease.

Determining the initial state of each individual, and the possible subsequent state, estimating the number of infections and possible loss of life, will allow governments to make predictions in the health systems, and develop a timely response to the disease that allows saving lives. Also, implement public policies in the education system, which will mitigate school closings and design fiscal policies that lessen the population's economic impact.

Epidemiological and economic charts.

The below image shows four curves, two curves in the upper quadrant (epidemiological curves), coordinate (Y) represented by the new cases of infections due to COVID-19. In this quadrant, the red curve is influenced by the containment policies' absence, where the disease infects a significant number of individuals. The blue curve in the upper quadrant is influenced by sanitary measures and social distancing implementing, showing a significant reduction of individuals infected by the COVID-19.

The two additional curves are showing the lower quadrant (economic curves) and coordinate (X) represented by periods of time (t). In this quadrant, the red curve is influenced by the containment policies' absence, where the disease motive a soft recession curve. However, the blue curve in the lower quadrant is influenced by sanitary measures and social distancing implementing, where the disease motive a significant recession curve.

Graph analysis

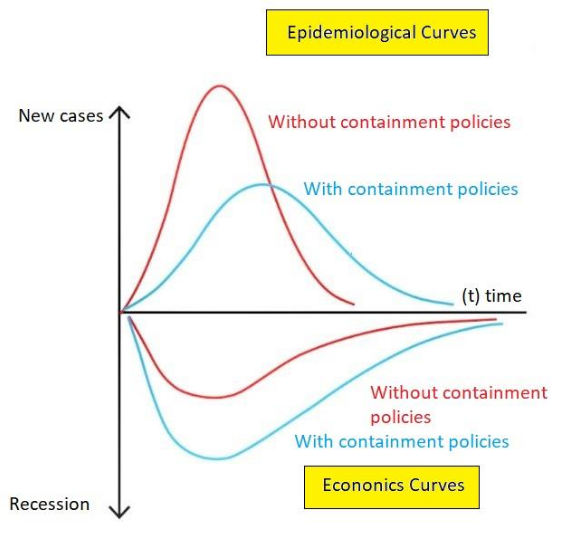
Graphs in the upper quadrant express the number of individuals infected in a period. However, Graphs within the lower quadrant express specific probabilities of an economic recession during that same period that the epidemiological cures occur, both options due upon COVID-19 pandemic.

In the upper epidemiological graph, a similarity can be observed in the behavior, which can be rectified, or softened over time if the containment measures are applied. In the lower economic graphs, behavior contrary to the epidemiological curves is observed, that is to say, with the strict implementation of the containment measures, the probabilities of a fall, or economic recession are accentuated.

The fundamental idea is to promote balanced policies that mitigate epidemiological and economic curves until the curves have a linear evolution or converge to zero in time.

CONCLUSION

Based on the hypotheses put forward, it is appropriate to conclude that the society and governments must be solidarities to face the COVID-19 pandemic, therefore enhancing population welfare. Governments must implement economic and health policies that slow down contagion and implement economic policies and fiscal support that prevent profound economic deterioration.

The governments should also consider the psychological effects on the population, due to confinement, and new patterns of social interaction, such as distancing, masks use, and gloves use. Especially in vulnerable populations due to age, pre-existing health conditions, socioeconomic status.

UNICEF has issued a large number of recommendations to continue educating children at home during the confinement and closure of schools. Measures such as implementing online education where possible, Teachers and parents should follow up on reading and educational exercises at home, teach and reinforce cleaning habits, address psychological support issues.

On the other hand, the expectation in the stock market maintains a tendency for volatile prices. Equity will be mobilized to areas where companies have remained open and with the expectation of increasing production, hiring employees, improving services. Furthermore, a significant part of the capital will remain protected in bonds and raw materials, such as silver and gold.

At the end of the day, whether the COVID-19 spreads in commonly repeated contagion patterns worldwide, it would give us an idea that we could analogously apply. Using behavior patterns and social distancing in the most affected regions; thus, reducing the spread and lessen the impact in a field as necessary as education.

REFERENCIAS